2020年之后的新版课程，由 Eric Demaine 主讲。 （2010年之前老视频中的二讲教授）
主讲：Prof. Eric Demaine, Dr. Jason Ku, Prof. Justin Solomon
课程主页：https://ocw.mit.edu/6-006S20

课程来自Bilibili地址

时间复杂度

• 大O表示法

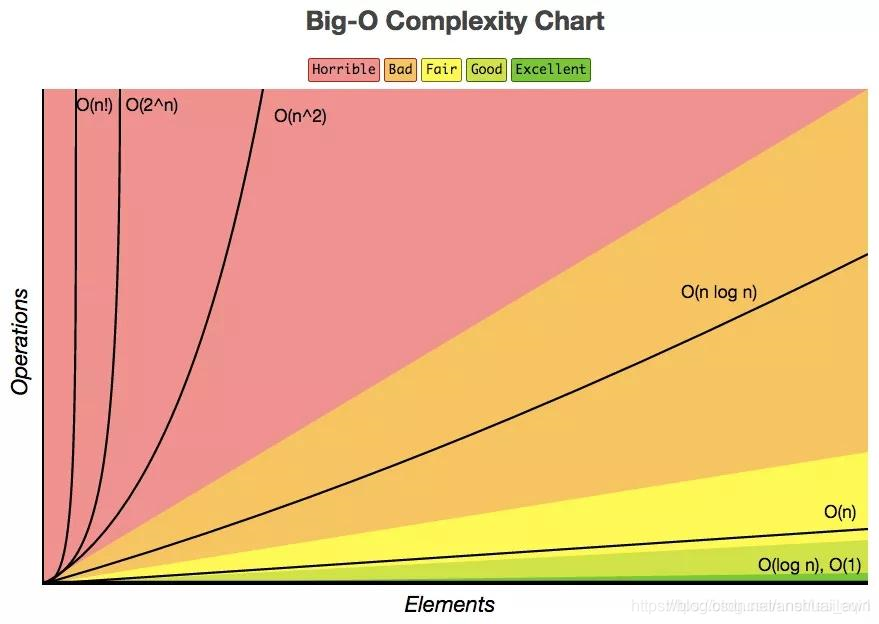
Sequence 数据结构
static array

静态数组的好处是知道 head 位置，　就知道它后面的所有位置的内存地址，那么对于“根据编号去访问”的场景，就去使用 array 。

随机访问(get、set random position) O(1)
构建(build) O(N)

插入 insert_at, 涉及原有元素的移动 O(N)
删除 delete_at , 涉及原有元素的移动 O(N)

数组快要满了，就要考虑扩容的策略　——
resize 设计　一般是乘数(multiple)扩容，而非常数扩容。　
（发散问题，　为什么要用　2 倍扩容，　而不是　＋5　扩容）　
（发散问题，什么时机扩容，　距离满容　80％　？　70％　？）

dynamic array (linked list)

item|next, next 是指向下一个元素的pointer.
build 成本　O(N)
insert_at 中间插入,先寻找插入位置, O(N), 如果只在头部位置, 成本就是O(1)
delete_at 　中间删除,先寻找插入位置, O(N), 如果只删除头部位置, 成本就是O(1)

QuickSort

(老版的视频资料)

Divide and Conquer (分治)

O(N) 的复杂度, 执行 partitioning ; 划分次数要执行 O(Log N)次

算法介绍:

i = p 
for j <- p+1 to q 
     do if A[j] <= x 
           then i = i + 1 
                      A[i] <-> A[j]
A[p]  <- A[i]

例题

Ex,  6, 10, 13, 5, 8, 3, 2, 11    x < -6 (pivot)
    j 遍历到5, 小于6 , 和10交换
6,  5, 13, 10, 8, 3, 2, 11
    j遍历到3 和13 交换
6, 5, 3, 10, 8, 13, 2, 11
    j遍历到2 和10交换
6, 5, 3, 2, 8, 13, 10, 11
    j遍历结束
最后再交换 A[i] 和pivot
 2,5,3,6,8,13,10,11   









 老版视频, 证明比较排序算法最好的复杂度就是 O(NlogN)

怎样在线性复杂度完成排序?

扩展介绍了几种别的非比较排序:
计数排序 counting sort 复杂度是 O(N+k) k 是输入数据的范围
基数排序 radix sort : digit by digit 排序, 复杂度是 O(N T) T 是有多少位

哈希碰撞

？

BST 二叉搜索树

好的搜索树 : 平衡 vs. 不好的搜索树,退化为链表

中序遍历, 第二次访问根节点时,对其打印输出.
时间开销, O(N)

数组 (N个元素) 建树的时间复杂度? (N log N)

定义,随机化二分搜索的树高度的期望为 log (N)

图论

Graph 由 节点和连接节点的边组成。

扩展：边是否带有方向，称为有向图和无向图； 以及边上是否带有一个数值（权重），权为有权图和无权图。

简单图： 没有自环，每条边都是唯一的，同一对顶点间只有一条边（或者没有）。

预留问题，网络中的最短路径如何求解？

最小权重路径如何求解？

单源路径（single source path)，给定一个入口节点，从这个节点出发，到其它任意节点的最短路径。

动态规划 DP